Homework 2:

Individual
 Due Date: September 22
Points: 55

  1. (10 points) Consider the following EBNF syntax.  Which if the sentences following are not legal according to the syntax for sneeches?  Why?
    sneech ::= '*' |
    ( '(' <sneech> ')' '*') |
    [ <bander>] <sneech>
    bander ::= { '+$+' | '#' } | ('%' <bander> )

    1. (*)  Not legal. A sneech enclosed in parentheses must have a * outside of the closing parenthesis.
    2. (+$+*)  Not legal. The * must be outside the closing parenthesis.
    3. *  Legal
    4. *****  Not legal. * is a terminal without a rule allowing repetition 
    5. %%%** Not legal. * is a terminal without a rule allowing repetition 
    6. #####** Not legal. * is a terminal without a rule allowing repetition 
    7. (+$+# Not legal. Must have a closing parenthesis. 
    8. +$+#* Legal
    9. *+$+# Not legal. There is no provision for a sneech followed by a bander.
    10.

    %#*+$+**

    		Not legal. * is a terminal without a rule allowing repetition.

  1. (5 points) Consider the grammar

    bexpr ::= bexpr or bterm | bterm
    bterm ::= bterm and bfactor | bfactor
    bfactor ::= not bfactor | (bexpr) | true | false

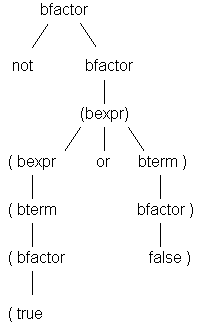
    Construct a parse tree for the sentence not (true or false).
    Show that this grammar generates all Boolean expressions.
    Parse Tree for: not (true or false)

    Parse Tree for not(true or false)

Proof that this language supports all Boolean expressions: 

 

bfactor=> bfactor

bfactor=> bfactor

           => TRUE

           => FALSE

 

 

bfactor r=>bfactor

bfactor=>bfactor

            => not bfactor

           => not bfactor

           => not TRUE

           => not FALSE

nor: 

 nand:

bfactor => not bfactor

bfactor => not bfactor

            => not ( bexpr )

            => not ( bexpr )

            => not ( bexpr or bterm )

            => not ( bterm )

            => not ( bterm or bterm )

            => not ( bterm and bfactor )

            => not ( bfactor or bterm )

            => not ( bfactor and bfactor )

            => not ( true or bterm )

            => not ( true and bfactor )

            => not ( true or bfactor )

            => not ( true and false )

            => not ( true or false )

 

 xor:

xnor: 

bexpr => bexpr or bterm

bexpr => bexpr or bterm

          => bterm or bterm

          => bterm or bterm

          => bfactor or bterm

          => bfactor or bterm

          => ( bexpr ) or bterm

          => ( bexpr ) or bterm

          => ( bterm ) or bterm

          => ( bterm and bfactor ) or bterm

          => ( bterm and bfactor ) or bterm

          => ( bfactor and bfactor ) or bterm

          => ( bfactor and bfactor ) or bterm

          => ( true and bfactor ) or bterm

          => ( true and bfactor ) or bterm

          => ( true and false ) or bterm

          => ( true and false ) or bterm

          => ( true and false ) or bfactor

          => ( true and false ) or bfactor

          => ( true and false ) or ( bexpr )

          => ( true and false ) or ( bexpr )

          => ( true and false ) or ( bexpr or bterm )

          => ( true and false ) or ( bexpr or bterm )

          => ( true and false ) or ( bterm or bterm )

          => ( true and false ) or ( bterm or bterm )

          => ( true and false ) or ( bfactor or bterm )

          => ( true and false ) or ( bfactor or bfactor )

          => ( true and false ) or ( false or bterm )

          => ( true and false ) or ( false and bfactor )

          => ( true and false ) or ( false or bfactor )

          => ( true and false ) or ( false and true )

          => ( true and false ) or ( false or true )

 

 

NOT is implemented by bfactor

OR is implemented by bterm

AND is implemented by bexpr

 

 

  1. (10 points) Consider the grammar:

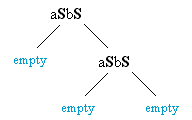
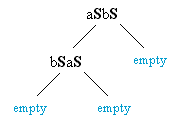
    S ::= aSbS | bSaS | empty

    Show that this grammar is ambiguous by constructing two different leftmost derivations for the sentence abab.

S ::= aSbS S ::= aSbS
  =>  a empty bS    =>  a bSaS bS
  => a empty b aSbS   => a b empty aS bS
  => a empty b a empty bS   => a b empty a empty bS
  => a empty b a empty b empty   => a b empty a empty b empty
 

=

 abab  

=

 abab


Construct the corresponding rightmost derivations for abab.

S

 ::= aSbS

S

 ::= aSbS
=>  aSb aSbS =>  aSb empty
=> aSb aSb empty => a bSaS b empty
=> aSb a empty b empty => a bSa empty b empty
=> a empty b a empty b empty => a b empty a empty b empty
= abab = abab


Construct the corresponding parse trees for abab.

              

 

  1. (30 points) Construct a grammar for if-then statements of each of the following languages:
    JavaScript

    <if_then>::= if (<Boolean_expression>) {

         {<command.something>( statement )}

    }

    [else {

        {<command.something>( statement )}

    }]
    Pascal

    <if_then>::= if <Boolean_expression> then

         begin

              { < Pascal statements > }

         end

    else

         begin

              { < Pascal statements > }

         end
    Prolog <if_then> := if ( (<ConditionGoal>, !), <ThenGoal>, <ElseGoal>)
    Lisp

    <test> ::= '('<Boolean_expression>')'

    <action> ::= '('<statement>')'

    <test set> ::= '('<test> <action>')' | <test set><test set>

    <if_then> ::= '(cond'  <test set>');'
    COBOL

    <if_then> ::= IF <Boolean_expression>

    THEN

        {<statement commands>}

    ELSE

         {<statement commands>}

    END-IF
    Simula <if_then> ::= if <condition> then
    begin
    [ <statements> ]
    end;
    else
    begin
    [ <statements> ]
    end;