Consider a discrete-time system described by a general, N-th order, linear constant-coefficient difference equation

A₀ y[n] + A₁ y[n-1] + ··· + A_N y[n-N] = B₀ x[n] + B₁ x[n-1] + ··· + B_M x[n-M]

YN = dtsim(B,A,XN,IC);

YZS = dtsim(B,A,XN,zeros(1,N));   % zero-state response
YZS = dtsim(B,A,XN);              % zero-state response
YZI = dtsim(B,A,zeros(1,K),IC);   % zero-input response for 0 ≤ n < K
YN = YZS + YZI;                   % total response
[YN,YZS,YZI] = dtsim(B,A,XN,IC);  % most general call (all three responses
                                  % in one shot)
HN = dtsim(B,A,[1 zeros(1,K-1)]); % impulse response to K terms

An alternative way for obtaining the impulse response h[n] of the system to K terms, i.e., over the index range 0 ≤ n < K is as follows:

HN = dtsim(B,A,K);

Before doing an example, there is one quirk of dtsim that needs to be noted: it requires the coefficient vectors A and B to be of the same length. The general form of the diffence equation given above assumes that the leading output and input terms are y[n] and x[n], respectively. Consequently, the corresponding coefficient vectors are understood to start as A = [ A₀ A₁ A₂ ... ] and B = [ B₀ B₁ B₂ ... ]. Any deviation from this general form would have to be reflected by including leading zero coefficients in A or B as needed. However, dtsim requires inclusion of trailing zeros as well so that both A and B have the same number of elements. Take the following examples illustrating this point (correct coefficient vectors are indicated by bold typeface):

y[n] = x[n-2]	···>	A = 1; A = [1 0 0];	B = [0 0 1]; B = [0 0 1];
y[n] = x[n+1]	···>	A = [0 1]; A = [0 1];	B = 1; B = [1 0];
y[n] - 2y[n-1] = x[n+1] + 2x[n] - x[n-2]	···>	A = [0 1 -2]; A = [0 1 -2 0];	B = [1 2 0 -1]; B = [1 2 0 -1];

Now, take the following example:

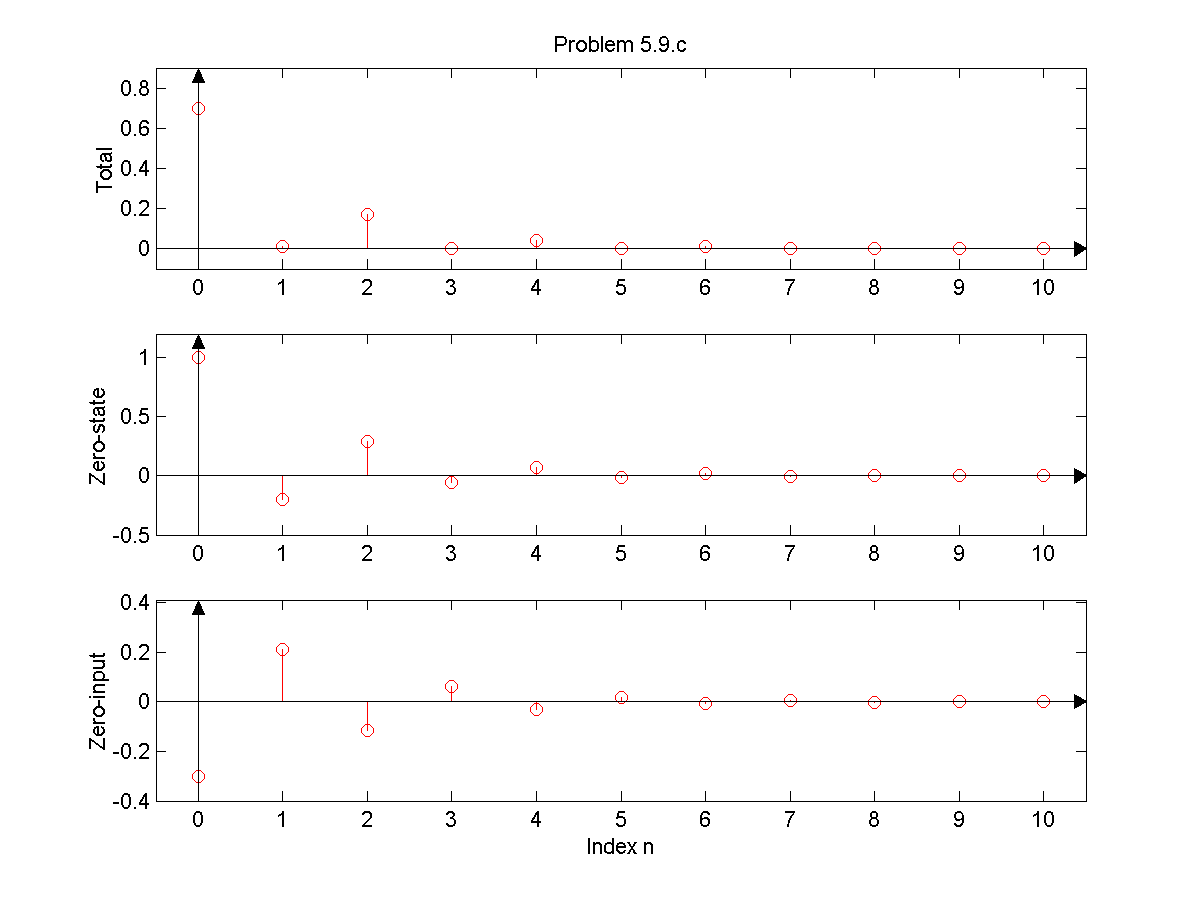
y[n] + 0.7y[n-1] + 0.1y[n-2] = x[n];    x[n] = (0.5)ⁿ u[n];    y[-1] = 0, y[-2] = 3.

>> n = 0:10; x = 0.5 .^ n;
>> [yt,yzs,yzi] = dtsim([1 0 0],[1 .7 .1],x,[0 3]);
>> figure(1); clf;
>> subplot(3,1,1);
>> dtplot(n,yt,'o'); ylabel('Total'); 
>> axis([-.5 10.5 -.1 .9]); axesn;
>> title('Problem 5.9.c');
>> subplot(3,1,2);
>> dtplot(n,yzs,'o'); ylabel('Zero-state');
>> axis([-.5 10.5 -.5 1.2]); axesn;
>> subplot(3,1,3);
>> dtplot(n,yzi,'o'); ylabel('Zero-input');
>> axis([-.5 10.5 -.4 .41]); axesn;
>> xlabel('Index n');

Also see the example below. Its about smoothing effects of a moving average filter. Exercise 4 in this assignment is about minimizing such undesired variations superimposed on a signal due to random noise. Filtering in general is a commonly used technique to minimize noise effects, and a moving average filter is probably the simplest form of filtering that could be used for this purpose. In Exercise 4, you will try out different forms of filtering for noise suppression.

Consider a 20 point moving average FIR filter y[n]=1/20{x[n]+x[n-1]+.....+x[n-19]}. It is also called a smoothing filter because it tends to smooth out the rapid variations in a signal. To confirm its smoothing property, try the following:

1. Generate 200 samples of a 1-Hz sine wave sampled at 40Hz.
2. Add some noise to generate a noisy signal.
3. Filter the noisy signal through the 20 point filter.
4. Plot each signal to display the effects of noise and smoothing.

n=0:199;
x=sin(2*pi*n*0.025); x=x(:);
xn=x+0.5*randist(x,'uni');
a=[1 zeros(1,19)];
b=0.05*ones(1,20);
y=filter(b,a,xn);
plot(n,x);
plot(n,xn,n,y);