| ECE 381: Laboratory 3 |
Winter 2006 |
| Touch-tone telephone dialing and music synthesis |
February 7 |
|
| Part II. Background discussion |
MATLAB notes | Background discussion |
Assignment |
|
DTMF dial signals:
In dual-tone multi-frequency (DTMF) or touch-tone telephone dialing,
each keypress is represented by a dual-frequency signal, which is called a dual-tone simply.
The mapping between the keys and the frequencies are as follows:
|
|
|
→ |
697 Hz |
|
|
|
→ |
770 Hz |
|
|
|
→ |
852 Hz |
|
|
|
→ |
941 Hz |
| ↓ |
↓ |
↓ |
|
| 1,209 Hz |
1,336 Hz |
1,477 Hz |
|
To be more precise, one can take the DTMF signal corresponding to a given key k to have the form
xk(t) = cos(2π fL t) + cos(2π fH t), where
fL and fH are the low and high frequencies
associated with the key k.
For key 6, for example,
x6(t) = cos(2π770t) + cos(2π1477t).
The composite DTMF signal for a sequence of keys, i.e., to a telephone number,
is obtained as the superposition of the individual, truncated and time-shifted dual-tones corresponding to
the numbers.
As would be expected from everyday experience with telephones,
truncation and time shifting of individual dual-tones is done in such a way that there is no overlapping
of successive dual-tones and there is a short silence between them.
So each dual-tone is heard distinctly.
When it comes to constructing the sampled representation of a composite DTMF signal in the lab,
the superposition task described above reduces to concatenation of sampled representations of individual
finite-duration dual-tones.
To represent silence between numbers, one simply inserts an appropriate number of zeros
between the sampled dual-tones.
Music synthesis:
A musical piece is a sequence of notes, which are essentially signals at various frequencies.
An octave covers a range of frequencies from a base pitch
f0 to twice the base pitch, 2f0.
In the western musical scale, there are 12 notes per octave, A through G# (or Ab),
and they are logarithmically equispaced
over the octave. That is, the frequency of the k-th note in a given octave with the base pitch of
f0 is equal to
fk = 2k/12f0,
k = 0, 1, 2, ..., 11.
This leads to the following integer encoding of notes within a given octave:
| Notes: |
A |
A# or Bb |
B |
C |
C# or Db |
D |
D# or Eb |
E |
F |
F# or Gb |
G |
G# or Ab |
| Integer k: |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
The superscripts "#" and "b" are read as sharp and flat, respectively, and
each pair of notes with the same integer code are meant to be at the same frequency.
Also observe that the above integer encoding naturally lends itself to representing
sequences of notes covering more than one octave.
That is, integers k < 0 and k > 11 indicate,
respectively, notes in a lower and higher octave with respect to the reference octave
starting at f0.
Thus, one can encode any musical piece as a sequence of integers, and construct a corresponding sampled signal
representation, provided that the reference base pitch f0 and
the duration of each note are all specified.
Similarly to the case of the DTMF dial signals, this entails concatenation of sampled signals
corresponding to individual notes.
As for the general form of the signal for a given note, one can consider a pure tone as the simplest form.
That is to say, for note D, for example, the form is
x5(t) = cos(2π f5t + θ).
Pure tones, however, will not sound as pleasant as one would like.
To add some color to the sound, consider the improved form
xk(t) = α(t)cos(2π fkt + θ),
where α(t) shapes the otherwise flat envelope of the pure tone signal.
This helps simulate the attack-sustain-release characteristics of different instruments, and
gives rise to overtones (harmonics) thus enriching the sound.
The following figure exemplifies the envelope forms α(t) and simulated
notes for woodwind- and string/keyboard-type instruments, where the duration of the note is normalized to unity.
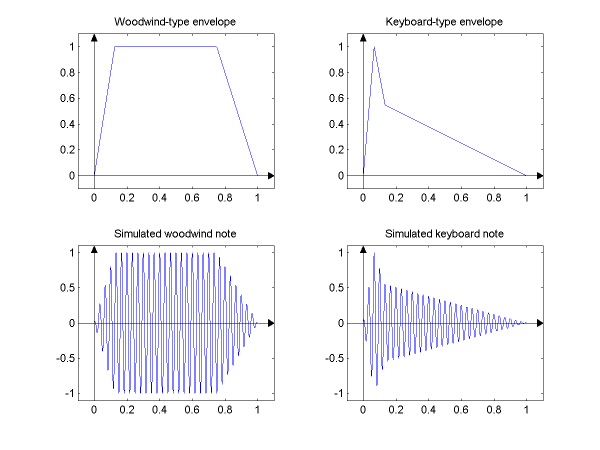
Can you tell from this figure the longer sustain characterictics of woodwind intruments as opposed to
the pronounced release (decay) characteristics of string or keyboard intruments?
General:
Recall, from the previous assignment, that MATLAB's sound function accepts the reconstruction
sampling frequency as an optional second argument.
If you do not pass this information to sound explicitly, the default sampling frequency of 8,192 Hz
is assumed.
In this experiment, you would do fine with this default value, without risking aliasing.
The highest frequency involved in the DTMF dialing case is 1,477 Hz, which is less than half of 8,192 Hz.
In the case of music synthesis, a base pitch of f0 = 440 Hz is the
standard choice that you might use, and even if you go as high as three octaves above this value, your highest
frequency will be 23·440 = 3,520 Hz, which is still less than half of 8,192 Hz.
Also recall that sound clips off portions of the input signal exceeding unity in absolute amplitude.
Make sure that your signals are normalized so that all sample values lie in the interval
[-1.0,1.0].
School of Computing and Engineering
University of Missouri - Kansas City
|
Last updated: February 05, 2006
|
