| ECE 381: Laboratory 5 | |
| Analog system response using ODE solvers | |
|
| |
|
| |
First a technical explanation: an ODE the solution of which contains a rapidly decaying transient term is said to be stiff. Accurate numerical solution of stiff ODEs requires a very small time step, and hence, it is in general difficult. However, the rapidity of such decay is relative to the time interval of interest on which the solution is sought, and it should not be a cause for concern in this assignment. That is, a non-stiff ODE solver, e.g., ode23, would be fine for you to work with. Here is the first help paragraph for this function.
>> help ode23
ODE23 Solve non-stiff differential equations, low order method.
[T,Y] = ODE23(ODEFUN,TSPAN,Y0) with TSPAN = [T0 TFINAL] integrates the
system of differential equations y' = f(t,y) from time T0 to TFINAL with
initial conditions Y0. Function ODEFUN(T,Y) must return a column vector
corresponding to f(t,y). Each row in the solution array Y corresponds to
a time returned in the column vector T. To obtain solutions at specific
times T0,T1,...,TFINAL (all increasing or all decreasing), use
TSPAN = [T0 T1 ... TFINAL].
The second argument TSPAN is understood from this much explanation as the time interval of interest. You either specify the end points of the interval, or pass a vector of all time instants at which you wish to obtain the solution value. The first and the third arguments, ODEFUN and Y0, describe the equation and the initial conditions, respectively, but they need some further explanation.
Matlab requires your n-th order differential equation (DE) to be presented as a system of n first-order DEs. So, a given DE is to be put in this form first. Take as an example a general second-order LCCDE with a single-term right-hand side and arbitrary initial conditions:
y''(t) + a1 y'(t) + a2 y(t) = x(t), where y(0) = y0 and y'(0) = y'0.
By defining
z1'(t) = z2(t) and z2'(t) = x(t) - a1 z2(t) - a2 z1(t), where z1(0) = y0 and z2(0) = y'0.
Now, ODEFUN, the first argument to ODE23, is a handler to a Matlab function that describes such a system of DEs. You need to write this function, and continuing with the same second-order example, here is what it should look like:
function dzdt = myfunc(t,z)
dzdt = [ z(2); {rhs}(t) - a1*z(2) - a2*z(1) ];
where {rhs} is a place holder for the forcing function
As for the outputs T and Y from ODE23, you will
find the desired solution in the first column of Y, ready to be plotted
against the time vector T:
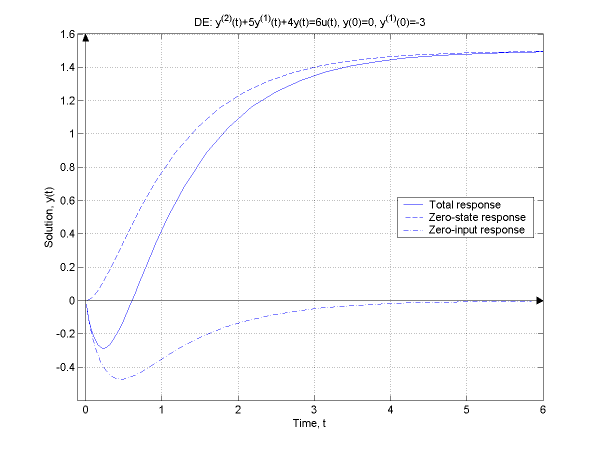
To make this more concrete take the following equation, the solution of which
is sought for
y''(t) + 5y'(t) + 4y(t) = 6u(t), where y(0) = 0 and y'(0) = -3.
The function you need to write for this is as follows:
function dzdt = mydiffeq(t,z) dzdt = [z(2); 6-4*z(1)-5*z(2)];
Now, you are ready to call the ODE solver for the problem:
function runexample(figureNo)
% Just putting everything in a function to avoid cluttering of the work
% and disk spaces.
figure(figureNo); clf;
% Find and plot the total response first.
[t,y] = ode23(@mydiffeq,[0 6],[0 -3]); % note the '@' symbol in front of
% the function name 'mydiffeq'
plot(t,y(:,1),'-'); % solid line for the total response
grid; hold on;
% Find and plot the zero-state and zero-input responses.
[t,y] = ode23(@mydiffeq,[0 6],[0 0]);
plot(t,y(:,1),'--'); % dashed line for the zero-state response
[t,y] = ode23(@mydiffeq0,[0 6],[0 -3]);
plot(t,y(:,1),'-.'); % dot-dashed line for the zero-input response
% Adjust and label the plots.
axis([-.1 6 -.6 1.6]); axesn;
title('DE: y^(^2^)(t)+5y^(^1^)(t)+4y(t)=6u(t), y(0)=0, y^(^1^)(0)=-3');
xlabel('Time, t'); ylabel('Solution, y(t)');
legend('Total response','Zero-state response','Zero-input response',0);
function dzdt = mydiffeq(t,z)
% Local function for finding the zero-state and total responses.
dzdt = [z(2); 6-4*z(1)-5*z(2)];
function dzdt = mydiffeq0(t,z)
% Local function for finding the zero-input response.
dzdt = [z(2); 0-4*z(1)-5*z(2)];
% -- end of runexample.m --------------------------------------------------
In this assignment, you are expected to obtain the solutions numerically as described above, using ode23.
| School of Computing and Engineering University of Missouri - Kansas City |
Last updated: February 20, 2006 |